はじめに
統計学は様々なデータ解析手法を提供しており、その中でも「t検定」は2つ標本の平均に差があるかを確認する際に利用される有力な手法の一つです。
この記事では、t検定の基本的な仕組みや、結果の解釈に関わる要素である有意差やp値について理解を深めていきましょう。
t検定も含め、多くの統計的検定があるため、ビジネス適用の際には適切な手法を選択することが重要です。もし難しいと感じる際は、経験豊富な方とマンツーマンで学習していくのもオススメです。
t検定の基本
t検定は、2つの標本の平均値が統計的に有意な差を示しているかどうかを評価する手法です。
例えば、新しい薬の効果を確かめるために、治療群と対照群の平均値を比較する場合などに使用されます。以下にt検定の基本的なステップを示します。
1. 帰無仮説と対立仮説の設定
帰無仮説(H0)は、標本の平均に差がないという仮説です。対立仮説(H1)は、逆に標本の平均に有意な差があるという仮説です。
2. t値の計算
標本から計算されるt値は、標本の平均値の差を標本のばらつきで調整したものです。このt値が大きいほど、差が有意である可能性が高まります。
1標本t検定
こちらは母集団と1標本を比較するt検定の式となります。
- \( t \):t値
- \( \bar{x} \):標本平均
- \( \mu \):母集団の平均
- \( s \):標本の不変標準偏差
- \( n \):標本のサイズ
2標本t検定(等分散の場合)
2つの独立した標本の平均を比較する際、2つの標本が同じ分散(等分散)を持つと仮定される場合は下記を利用します。
- \( t \):t値
- \( \bar{x_1} \):標本1の平均
- \( \bar{x_2} \):標本2の平均
- \( n_1 \):標本1のサイズ
- \( n_2 \):標本2のサイズ
- \( s_p^2 \):プールされた分散(標本1の不変分散\( s_1^2 \)標本2の不変分散\( s_2^2 \)の加重平均)
プールされた分散は以下の通りです。
2標本t検定(ウェルチのt検定、等分散ではない場合)
2つの独立した標本の平均を比較する際、2つの標本が同じ分散(等分散)を持たないと仮定される場合は下記を利用します。
- \( t \):t値
- \( \bar{x_1} \):標本1の平均
- \( \bar{x_2} \):標本2の平均
- \( s_1^2 \):標本1の不変分散
- \( s_2^2 \):標本2の不変分散
- \( n_1 \):標本1のサイズ
- \( n_2 \):標本2のサイズ
上記3式の違いは「母集団から抜き出した標本が母集団と同じような集団か」「抜き出した2標本が同じような集団か(母分散が同じor違う)」を比較するためのt値計算になります。
3. 自由度の考慮
t値の有意性を評価する際には、自由度も考慮する必要があります。自由度は標本サイズに依存し、サンプルサイズが大きいほど自由度が増えます。
4. t分布表の利用
計算されたt値と自由度をもとに、t分布表を用いてp値を求めます。
5. 結果の判断
p値が事前に設定した有意水準(通常は0.05)よりも小さい場合、帰無仮説を棄却し、対立仮説を採択します。これは、2つの平均に統計的に有意な差があると解釈されます。
有意差の意味
有意差(statistical significance)は、標本から計算された統計量が偶然ではなく、真の差異を反映している可能性があることを示します。
t検定で有意差が得られた場合、標本の平均に統計的に有意な差があると考えられます。ただし、有意差が得られなかった場合でも、差がないと結論するわけではありません。注意が必要です。
p値の意味
p値(probability value)は、帰無仮説が正しいと仮定した場合に、計算された統計量以上の極端な結果が得られる確率を示します。
p値が小さいほど、帰無仮説を棄却する傾向が強まります。通常、p値が0.05以下であれば、統計的に有意な差があると判断されますが、この有意水準は実施する用途によって変わることがあります。
サンプルデータを用いた検定
実際に2つの分布を比較し、p値を算出しています。p値が0.05以下であり、2つの分布では統計的な差異があることが分かります。
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
# サンプル数
sample_size = 1000
# サンプルデータを作成します
group1 = np.random.normal(loc=10, scale=5, size=sample_size) # 平均10、標準偏差5の正規分布に従うデータを生成
group2 = np.random.normal(loc=12, scale=5, size=sample_size) # 平均12、標準偏差5の正規分布に従うデータを生成
# t検定を実行します
t_statistic, p_value = stats.ttest_ind(group1, group2)
# グラフを描画します
plt.figure(figsize=(8, 6))
plt.hist(group1, bins=30, alpha=0.5, label='Group 1', color='blue', density=True)
plt.hist(group2, bins=30, alpha=0.5, label='Group 2', color='orange', density=True)
# 近似線を追加します
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p1 = stats.norm.pdf(x, np.mean(group1), np.std(group1))
plt.plot(x, p1, 'blue', linestyle='dashed', linewidth=2)
p2 = stats.norm.pdf(x, np.mean(group2), np.std(group2))
plt.plot(x, p2, 'orange', linestyle='dashed', linewidth=2)
plt.xlabel('Value')
plt.ylabel('Density')
plt.title('Histogram with Normal Approximation of Group 1 and Group 2')
plt.legend()
plt.grid(True)
plt.show()
# 結果を出力します
print("t検定統計量 (T-statistic):", t_statistic)
print("p値 (P-value):", p_value)
# p値を元に結果を判定します
alpha = 0.05 # 有意水準を設定します
if p_value < alpha:
print("統計的に有意な差があります")
else:
print("統計的に有意な差がありません")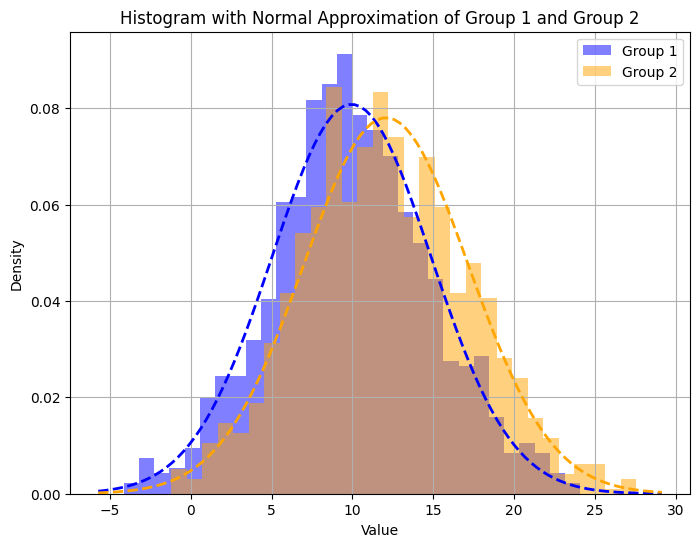

まとめ
t検定は標本の平均を評価するための強力な統計手法であり、有意差やp値はその結果を解釈する上で重要な指標です。
有意差が得られた場合、差が偶然ではなく、統計的に信頼できるものである可能性が高まります。
しかし、p値や有意差だけで結論を出すのではなく、研究の背景や文脈を考慮しながら検討することが重要です。
似たような手法にマンホイットニーのU検定もありますので、そちらも学習することをオススメします。
t検定を学ぶのにオススメの方法
書籍:データ分析に必須の知識・考え方 統計学入門
統計学を体系的に学びたい方には以下の書籍がオススメです。t検定以外にも多くの統計手法を入門者向けに記載されているのでこちらの書籍で学習することをオススメします。
資格:統計検定を受験する
統計検定は統計学の学習に最適です。2級以上を持っていることで転職などにも有利になるでしょう。私も3級→2級→準1級と取っていますが、かなり多くの知識を学ぶことができました。準1級の記事を記載しているので参考にしてみてください。





コメント