擬似相関とは。データ間の正しい関係を見極める

はじめに

データ分析において最も注意すべき落とし穴の一つが「擬似相関」です。

相関関係があるからといって因果関係があるとは限りません。この基本原則を理解せずにデータを解釈すると、間違った分析結果が得られることがあります。

この領域は複雑で理解が難しいですが、これらについて理解が難しい場合は、経験豊富な方とマンツーマンで学習していくのもオススメです。

擬似相関とは、二つの変数間に統計的な相関関係は観察されるものの、実際には直接的な因果関係が存在しない現象を指します。

つまり、「変数XとYの間に高い相関係数が観察されるにもかかわらず、XがYの直接的な原因でも、YがXの直接的な原因でもない状況」です。

ピアソンの相関係数は以下の式で計算されます。

$$ r = \frac{\sum (X_i-\bar{X})(Y_i-\bar{Y})}{\sqrt{\sum (X_i-\bar{X})^2 \sum (Y_i-\bar{Y})^2}} $$

この相関係数が高く、直線的な関係がみられる場合にも擬似相関が含まれている可能性があります。

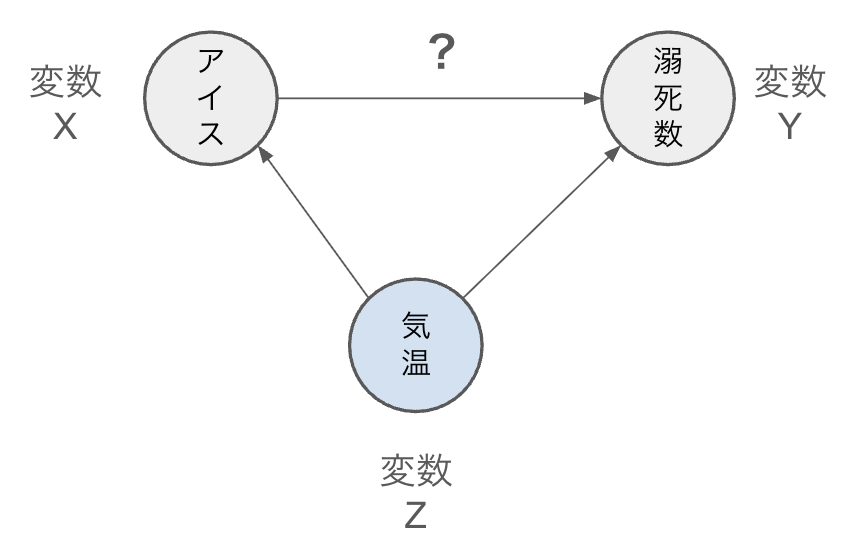
最も典型的なケースは、観察される二つの変数が共通の第三の変数Zによって影響を受けている場合です。

この場合、X ← Z → Y という関係性が成立し、XとYの間には直接的な因果関係がないにも関わらず相関が観察されます。

例えば、アイスクリームの売上と溺死者数には正の相関がありますが、これは気温という第三の変数が両方に影響を与えているためです。

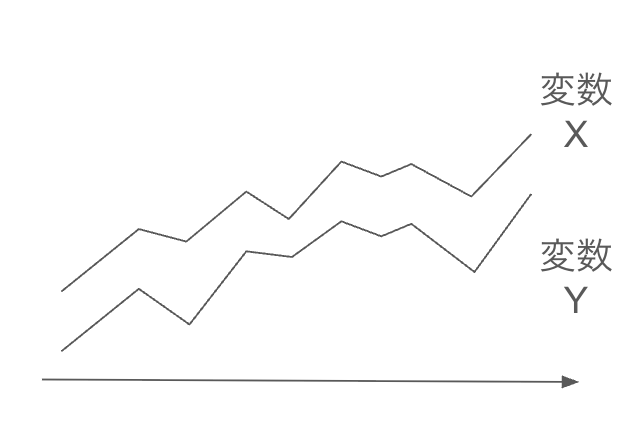
時系列データにおいて、両方の変数が同じ方向のトレンド（上昇傾向や下降傾向）を持つ場合、実際には無関係であっても高い相関が観察されることがあります。

例えばGDPや株価に連動するような2変数のX, Yをみていた場合、どちらも似たような傾向を示す場合があります。

特に相関がない場合もデータ間で偶然に相関があることも発生します。

下記の書籍などでは、「ある年のニコラス・ケイジの映画出演本数」と「その年のプールでの溺死数」に相関があることが紹介されています。

created by Rinker

こちらはデータというより背景をしっかりと把握するということになります。多くの場合、その業界の方がデータを見れば、おかしなデータ間で相関係数が高いとなっても変数自体を除外することができます。

まずは「擬似相関」の概念を理解し、リスクを把握することが重要です。その上でこのステップを踏むこと重要です。

第三の変数Zの影響を除去した偏相関係数を計算することで、2変数の相関関係を検証できます。

$$ r_{XY \cdot Z} = \frac{r_{XY} – r_{XZ}r_{YZ}}{\sqrt{(1-r_{XZ}^2)(1-r_{YZ}^2)}} $$

偏相関係数が大幅に減少する場合、元の相関は擬似相関である可能性が高くなります。

可能であれば統制された実験やランダム化比較試験（RCT）を実施することで、因果関係の存在を直接検証できます。

擬似相関はデータ分析において注意すべき課題です。

「相関は因果を意味しない」という原則を常に念頭に置き、統計的手法とドメイン知識を組み合わせた慎重な分析が求められます。

関係者なども巻き込みながら分析し、しっかりと意味ある分析を実施していきましょう。

擬似相関だけでなく、分析全般の手法を学ぶと言ったら初心者の方でもわかりやすいコチラの書籍オススメとなります。

created by Rinker

ただ、どのように分析するかを判断するには適切なメンターなどがいた方が安心です。スクールなどに入り、アドバイスしてもらいながら進めるのも良いでしょう。