はじめに
Ridge回帰は統計的なモデリングや機械学習において広く利用される手法の一つです。この手法は、線形回帰の一般化として知られており、特に多重共線性が存在する場合に効果的です。
本記事では、Ridge回帰の特徴、メリット、およびデメリットについて詳しく解説します。
Ridge回帰だけでなく、単純な回帰分析やLasso回帰など様々な予測手法は多く存在しているため、きちんと学ぶにはスクールなどに通うこともオススメです。
Ridge回帰とは
リッジ回帰は、線形回帰の目的関数に正則化項を追加することで、回帰係数の大きさを抑制し、モデルの複雑さを制御します。これにより、過学習のリスクを低減し、予測精度を向上させることができます。
通常の線形回帰
通常の線形回帰では、以下の損失関数を最小化します。
\( y_i \)は実際の値で、\( \hat{h}_i \)は予測値です。
Ridge回帰
これに対してRidge回帰は、L2正則化項を追加した損失関数を最小化します。
\( \alpha \)は正則化パラメータで、\( \beta_j \)はj番目の回帰係数です。
このように回帰係数が最小化するパラメータに入っているため、回帰係数が小さいモデルが適合しやすくなります。
\( \lambda \)も重要なパラメータであり、大きくするほど係数が小さくなりやすくなり、過学習抑制が強くなります。このパラメータは結果をみながら調整するのが必要です。
Ridge回帰の特徴
- 正則化項の追加: Ridge回帰は、通常の最小二乗法にL2正則化項を追加した形で表現されます。この正則化項は、係数の大きさにペナルティを課すことで、モデルの過学習を抑制します。
- 多重共線性への対処: Ridge回帰は、説明変数間に高い相関(多重共線性)がある場合に特に有効です。通常の線形回帰ではこのような状況が問題となりやすいが、Ridge回帰は安定性を提供します。
- 重みの縮小: Ridge回帰は係数(重み)を縮小するため、モデルがノイズに敏感になりにくくなります。これにより、一般化性能が向上し、未知のデータに対する予測精度が高まります。
Lasso回帰ではL1正則化項を用いて、いくつかの係数を0にします。こちらとも使い分けが必要です。

Ridge回帰のPython実装
糖尿病患者のデータセットを用いて単純な線形回帰とRidge回帰で予測してみます。6つの血液検査項目を入力とし、1年後の進行状況を予測ターゲットにします。
scikit-learnでは\( \lambda \)項が\( \alpha \)として実装されています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_diabetes
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
# データ読み込み
diabetes = load_diabetes()
X = diabetes.data
y = diabetes.target
feature_names = diabetes.feature_names
# データの標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 訓練・テストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
# 1. 通常の線形回帰
lr = LinearRegression()
lr.fit(X_train, y_train)
lr_score = lr.score(X_test, y_test)
# 2. Ridge回帰(異なるαで)
ridge_01 = Ridge(alpha=0.1)
ridge_01.fit(X_train, y_train)
ridge_01_score = ridge_01.score(X_test, y_test)
ridge_1 = Ridge(alpha=1.0)
ridge_1.fit(X_train, y_train)
ridge_1_score = ridge_1.score(X_test, y_test)
# 係数をまとめる
results = pd.DataFrame({
'特徴量': feature_names,
'線形回帰': lr.coef_,
'Ridge α=0.1': ridge_01.coef_,
'Ridge α=1.0': ridge_1.coef_,
})
# 係数の大きさ(L2ノルム)を比較
l2_linear = np.sqrt(np.sum(lr.coef_**2))
l2_ridge_01 = np.sqrt(np.sum(ridge_01.coef_**2))
l2_ridge_1 = np.sqrt(np.sum(ridge_1.coef_**2))
# グラフで可視化
plt.figure(figsize=(8, 6))
# 係数の値を棒グラフで比較
x_pos = np.arange(len(feature_names))
width = 0.2
plt.bar(x_pos - width*1.5, lr.coef_, width, label='線形回帰', alpha=0.8)
plt.bar(x_pos - width*0.5, ridge_01.coef_, width, label='Ridge α=0.1', alpha=0.8)
plt.bar(x_pos + width*0.5, ridge_1.coef_, width, label='Ridge α=1.0', alpha=0.8)
plt.xlabel('特徴量')
plt.ylabel('係数の値')
plt.title('線形回帰 vs Ridge回帰の係数比較')
plt.xticks(x_pos, feature_names, rotation=45)
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()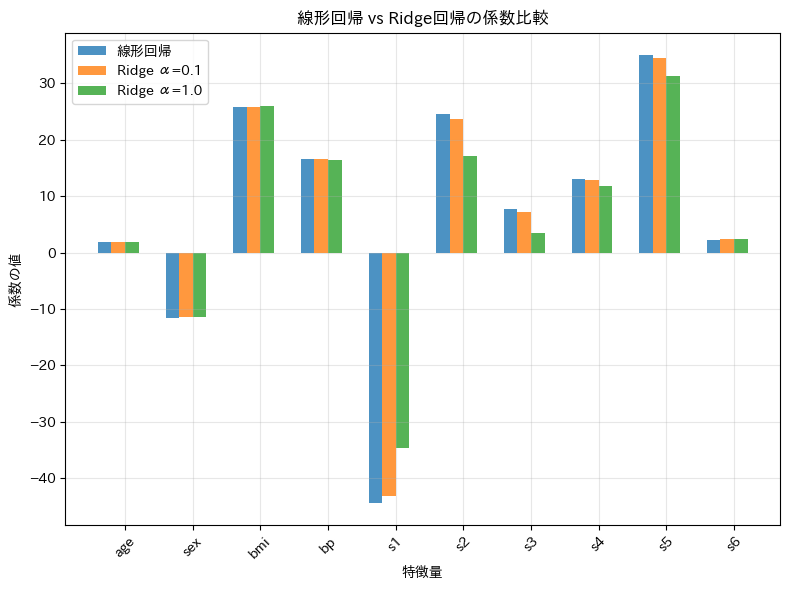
\( \alpha \)が大きくなると回帰係数が小さくなっていることがわかります。
まとめ
まとめると、Ridge回帰は多重共線性への対処や過学習の制御に優れた手法ですが、正則化パラメータの調整や解釈性の低下に注意する必要があります。
適切な状況で使用することで、高い予測性能を発揮することが期待されます。
Ridge回帰を学ぶのにオススメの方法
Python機械学習プログラミング 達人データサイエンティストによる理論と実践
少し厚い書籍となりますが、網羅的に分析手法がまとめられており、中級~上級に進みたいにはぜひともオススメしたい書籍となります。
スクール:現役データサイエンティストに教えてもらう
Ridge回帰などの様々な回帰分析は様々な場面で活用されるため、網羅的に学習することがオススメです。
ただ、どのようにやるのが正しいのかを判断するには適切なメンターなどがいた方が安心です。スクールなどに入り、アドバイスしてもらいながら進めるのも良いでしょう。





コメント