はじめに
データ分析の中でも特に重要な手法の一つである「回帰分析」について解説します。本記事では、初心者でもわかりやすいように、具体的な例や図を交えながら、その基本概念や使い方をわかりやすく説明します。
回帰分析など、様々な数値データを表現する方法は多く存在します。その際にどのモデルが最適かを理解していることがビジネス適用において非常に重要です。これらについて、経験豊富な方とマンツーマンで学習していくのもオススメです。
回帰分析とは?
回帰分析とは、データ間の関係性を明らかにする統計手法です。特に、目的変数(予測したい値)と説明変数(目的変数に影響を与える要因)の関係を分析するために用いられます。
例えば、次のようなシチュエーションを考えてみましょう。
- 気温が上がると、アイスクリームの売上も増えるのか?
- 広告費を増やすと、売上がどれだけ増えるのか?
このような課題を解決していくのが回帰分析です。
回帰分析の基本公式
単回帰分析
回帰分析では目的変数や説明変数を設定していきます。その中で算出される単回帰分析の式は下記のようになります。
- 目的変数(例:売上)
- 説明変数(例:広告費)
- 回帰係数(説明変数が1単位増加するときのの増加量)
- 切片(説明変数が0のときのの値)
- 誤差項(説明しきれない部分)
重回帰分析
また、説明変数が複数ある場合には重回帰分析を用います。その場合の式は以下のようになります。
実例:広告費と売上の関係を分析
具体的なデータを使って回帰分析を行ってみましょう。以下のデータは架空の広告費(万円)と売上(万円)です。
| 広告費 (x) | 売上 (y) |
|---|---|
| 10 | 25 |
| 15 | 30 |
| 20 | 40 |
| 25 | 45 |
| 30 | 50 |
| 35 | 55 |
| 40 | 60 |
| 45 | 65 |
| 50 | 70 |
| 55 | 75 |
ステップ1:データのプロット
まず、データを散布図にプロットします。横軸を広告費、縦軸を売上とすると、データ点が直線的な関係を持っていることがわかります。

ステップ2:回帰直線を求める
このデータに単回帰分析を適用して、回帰直線を求めます。計算の結果、次のような回帰式が得られたとします。
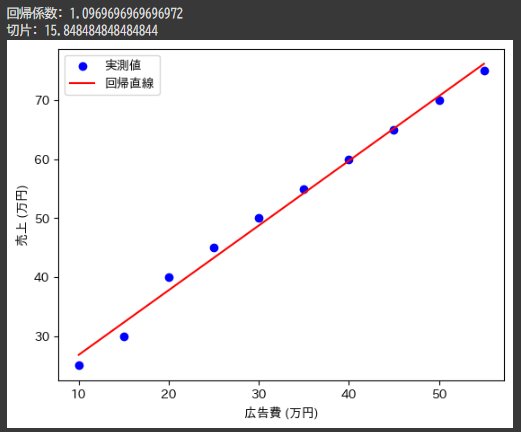
- 回帰係数1.096
- 切片15.84
この算出結果は、広告費が1万円増えるごとに売上が1.096万円増加することを意味します。
算出結果を用いて回帰線を引くと、よくフィットしていることが分かります。
ステップ3:予測
例えば、広告費を20万円に設定した場合の売上を予測すると、
と予測されます。実際のデータとも大体一致していました。
回帰分析の注意点
回帰分析を利用する際には、以下の点に注意が必要です。
- 多重共線性:複数の説明変数を使う場合、説明変数同士が強い相関を持つと、モデルが不安定になります。
- 外れ値の影響:データに外れ値が含まれると、回帰直線が大きく影響を受けることがあります。
- 因果関係の誤解:回帰分析はあくまで相関関係を示すものであり、因果関係を証明するものではありません。
Pythonで回帰分析を実装してみよう
以下は、Pythonを使った回帰分析の例です。データとしては同じものを使っています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# データの準備
x = np.array([10, 15, 20, 25, 30, 35, 40, 45, 50, 55]).reshape(-1, 1)
y = np.array([25, 30, 40, 45, 50, 55, 60, 65, 70, 75])
# モデルの作成
model = LinearRegression()
model.fit(x, y)
# 回帰係数と切片
print(f"回帰係数: {model.coef_[0]}")
print(f"切片: {model.intercept_}")
# 予測
predicted = model.predict(x)
# プロット
plt.scatter(x, y, color='blue', label='実測値')
plt.plot(x, predicted, color='red', label='回帰直線')
plt.xlabel('広告費 (万円)')
plt.ylabel('売上 (万円)')
plt.legend()
plt.show()
まとめ
回帰分析は、データの関係性を理解し、将来の予測を行うための強力な手法です。本記事では、基本的な概念から具体的な例、実装方法までをわかりやすく紹介しました。実際の分析に活用して、データの洞察を深めてみてください。
これらの回帰手法の結果をしっかり理解するためには決定係数なども見ながら評価する必要があるので、そちらも学習しましょう。
回帰分析を学ぶのにオススメの方法
書籍:多変量解析法入門
回帰分析だけでなく、決定係数などの評価方法もあわせて体系的に学びたい方には以下の書籍がオススメです。実際の数式が分かりやすく記載されており、しっかりと理解することができます。
スクール:現役データサイエンティストに教えてもらう
回帰分析はデータ分析で基礎的かつ重要な部分となります。ただ、どのようにやるのが正しいのかを理解しながら進めるには適切なメンターなどがいた方が安心です。スクールなどに入り、アドバイスしてもらいながら進めるのも良いでしょう。





コメント