分布を確認できる「Q-Qプロット」とは。視覚的に分布の比較をしよう

はじめに

データ分析において、データがどのような分布に従っているかを理解することは極めて重要です。

多くの統計手法は特定の分布（特に正規分布）を前提としており、この前提が満たされないと分析結果の信頼性が大きく損なわれる可能性があります。そこでよく用いられる手法が「Q-Qプロット」です。

データ分析の際にはしっかりと分布を確認しながら適切な方法を進めていくことが重要です。これらについて、経験豊富な方とマンツーマンで学習していくのもオススメです。

Q-Qプロット（Quantile-Quantile Plot）は、2つの確率分布の分位点を比較するための手法です。

分位点とは、データを小さい順に並べたときに、全体の何パーセント位置にあるかを示す値のことで、中央値は50パーセント位置の分位点に相当します。

Q-Qプロットでは、一方の分布の分位数をx軸に、もう一方の分布の分位数をy軸にプロットし、散布図として表示します。この手法により、2つの分布がどの程度似ているかを視覚的に判断することができます。

イメージをつけるために下記のようにステップごとにみます。今回はあるデータが正規分布に従っているか、「データ」と「正規分布」を比較します。

観測データを小さい順に並べ替えます。データ数をnとすると、1番目からn番目までの並べ替えます。

各データポイントに対応する分位点を計算します。下記のデータを左からデータを見ていき何%の位置にどの数値があるかを並べていきます。

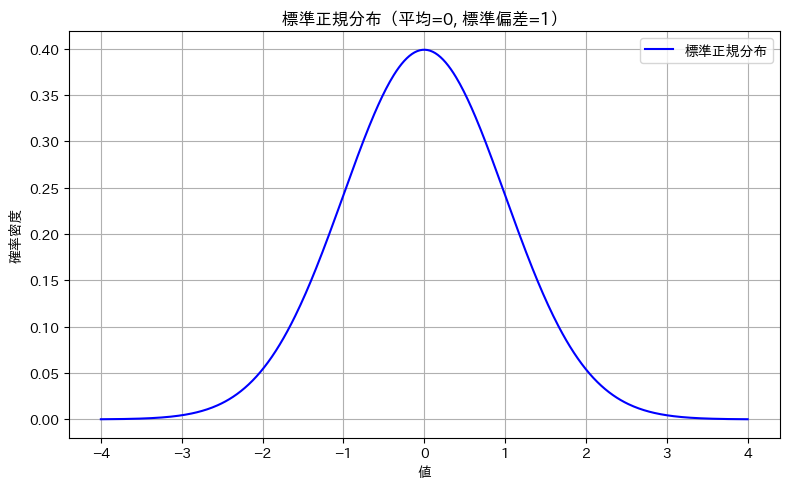
上記の小さい値から順々にデータ拾っていきつつ、下記の標準正規分布も同じ通りに同じ地点でデータを拾います。

という風に下記の標準正規分布から数値を取得していきます。今回のデータは下記の正規分布とよく似ているので、そのような結果が出そうです。

x軸に標準正規分布の分位点、y軸に実際の観測値の分位点をプロットします。データが正規分布に従う場合、これらの点は直線状に並びます。

正規Q-Qプロットは、サンプルデータが正規分布に従うかどうかを確認することができます。これは、実際のデータの分位数を理論的な正規分布の分位数と比較します。

正規性の確認は、t検定、回帰分析など、多くの統計手法で重要な前提条件となります。

これらの手法は正規分布を仮定しているため、データが正規分布から大きく逸脱している場合、分析結果が信頼できないものになってしまいます。

2つの異なるデータセットが同じ分布に従うかどうかを比較する際に使用します。

2つのデータの比較を行うこと収集したデータが期待される分布に従っているかを確認することができ、プロセスの異常やデータ収集の妥当性を評価できます。分布からの逸脱が発見されれば、プロセスや測定方法の見直し、早期に検討することが可能になります。

こちらも同じように分位数を揃えて散布図としてプロットすることで確認できます。

Q-Qプロットは、データの分布を視覚的に理解するための強力で直感的なツールです。統計分析の前提条件を確認したり、データの特性を把握したりする際に、数値では見えない分布の特徴を明確に示してくれます。

多くの分析は正規分布を仮定しているので、今回のQ-Qプロットなどを用いてしっかりとデータの分布なども調べてから、本格的な分析を実施していきましょう。

初学者が正規分布などに加えて、統計学を網羅的に学ぶには下記の書籍がオススメです。多くの図が含まれているため、初学者であっても非常に理解しやすいです。

created by Rinker

分布を適切に理解することはデータ分析で基礎的かつ重要な部分となります。ただ、どのようにやるのが正しいのかを理解しながら進めるには適切なメンターなどがいた方が安心です。スクールなどに入り、アドバイスしてもらいながら進めるのも良いでしょう。