はじめに
マハラノビス距離(Mahalanobis Distance)は、データのばらつきや相関関係を考慮して距離を測る方法です。
ユークリッド距離(単純な直線距離)と異なり、異なるスケールを持つデータや変数間の相関を考慮して正確に距離を測ることができるため、異常検知やクラスタリングの際に非常に有効です。
マハラノビス距離だけでなく、様々な距離指標や類似度指標がありますが、適切な手段を使って進めていくことが重要です。これらについて、経験豊富な方とマンツーマンで学習していくのもオススメです。
マハラノビス距離の数式
マハラノビス距離は以下の数式で定義されます。
- \( D_M \)はマハラノビス距離
- \( x \)は観測データのベクトル
- \( \mu \)はデータの平均ベクトル
- \( S^{-1} \)は共分散行列の逆行列
マハラノビス距離の具体例:従業員の身長と体重データ
以下のデータセットを用いて、マハラノビス距離を計算します。
| 従業員 | 身長 (cm) | 体重 (kg) |
| A | 170 | 65 |
| B | 160 | 55 |
| C | 175 | 60 |
| D | 180 | 75 |
| E | 165 | 63 |
| F | 172 | 64 |
| G | 178 | 72 |
| H | 162 | 60 |
| I | 177 | 69 |
| J | 169 | 63 |
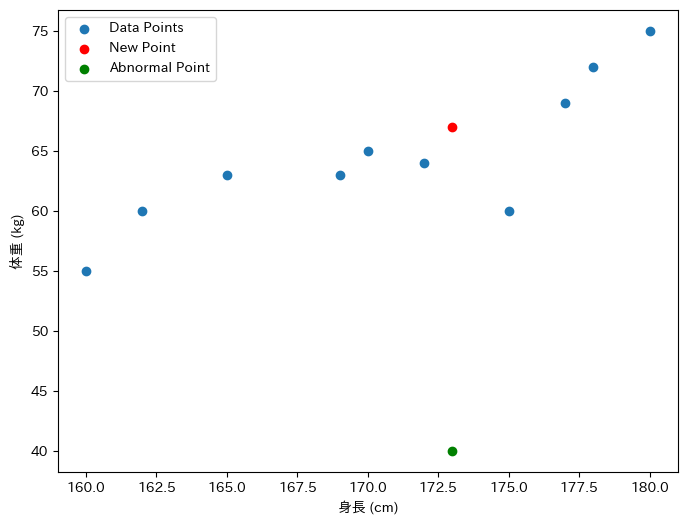
上記のデータ点は青として、それと赤(New Point)もしくはと緑(Abnormal Point)とのマハラノビス距離を計算していきます。
青のデータ点から離れている緑(Abnormal Point)のマハラノビス距離が大きくなるはずです。
ステップ1: 平均ベクトルの計算
まず、青データに関して、身長と体重の平均値を計算します。
| データ | 平均身長 (cm) | 平均体重 (kg) |
| 平均値 | 170.8 | 64.6 |
ステップ2: 共分散行列の計算
次に、青データに関して、身長と体重の共分散行列を計算します。
| 身長 (cm) | 体重 (kg) | |
| 身長 (cm) | \( \sigma_{\text{height}}^2 \\ = 47.289 \) | \( Cov_{height, weight} \\ = 34.689 \) |
| 体重 (kg) | \( Cov_{height, weight} \\ = 34.689 \) | \( \sigma_{\text{weight}}^2 \\ = 35.822 \) |
具体的な値を代入すると以下のようになります。
ステップ3: 共分散行列の逆行列の計算
次に、青データに関して、共分散行列\( S \)の逆行列\( S^{-1} \)を計算します。
| 身長 (cm) | 体重 (kg) | |
| 身長 (cm) | 0.073 | -0.071 |
| 体重 (kg) | -0.071 | 0.096 |
具体的な値を代入すると以下のようになります。
ステップ4: マハラノビス距離の計算
次に、新しいデータ\( x = (173, 67) \)が平均値からどれだけ離れているかをマハラノビス距離で計算します。
| 身長 (cm) | 体重 (kg) | |
| 平均値との差(\( x – \mu \)) | 173 – 170.8 = 2.2 | 67 – 64.6 = 2.4 |
これらを使って、マハラノビス距離を計算します。
具体的に、\( x – \mu = (2.2, 2.4) \)なので、この差を用いて次のように計算します。
計算結果として、\( D_M \)は約0.402になりました。
Pythonでのマハラノビス距離の計算
この手計算をPythonで実際に計算し、結果を確認してみましょう。
import numpy as np
from scipy.spatial import distance
# 身長と体重のデータ
data = np.array([[170, 65], [160, 55], [175, 60], [180, 75],
[165, 63], [172, 64], [178, 72], [162, 60],
[177, 69], [169, 63]])
# 平均値を計算
mean = np.mean(data, axis=0)
# 共分散行列を計算
cov_matrix = np.cov(data.T)
# 共分散行列の逆行列を計算
inv_cov_matrix = np.linalg.inv(cov_matrix)
# 新しいデータ点 赤のNew Point
x_new = np.array([173, 67])
# マハラノビス距離の計算
mahalanobis_distance = distance.mahalanobis(x_new, mean, inv_cov_matrix)
print(f"マハラノビス距離: {mahalanobis_distance}")同じように青 – 赤マハラノビス距離は約0.402となりました。
次に体重が極端に小さいサンプルを入れてみます。
# 異常値 緑のAbnormal Point
x_abnormal = np.array([173, 40])
# マハラノビス距離の計算
mahalanobis_distance = distance.mahalanobis(x_abnormal, mean, inv_cov_matrix)
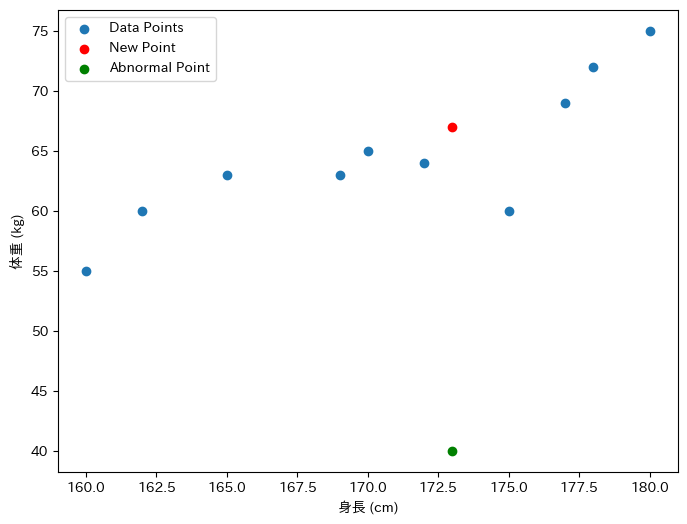
print(f"マハラノビス距離: {mahalanobis_distance}")異常値のような値を入れると青 – 緑のマハラノビス距離は8.144となり、非常に大きな値を出力しました。
実際に緑ポイントの異常値は大きく外れていることが分かります。
まとめ
マハラノビス距離は、データのスケールや変数間の相関関係を考慮した距離測定方法です。このブログ記事では、実際のデータセットを使って具体的な計算過程を解説しました。
距離指標として「ユークリッド距離」や「マンハッタン距離」もありますので、そちらも学習することをおススメします。
距離指標は類似指標は多く存在しますが、ビジネス活用場面でどれを使うのか選択するのが難しい場面が多くあります。スクールなどに入り、しっかりメンターに学びながら勉強することもおススメします。




コメント