はじめに
データ分析の際には、「Yes/No」「成功/失敗」「合格/不合格」といった2値(バイナリ)データを分析する場面は多く存在します。このような問題を分析する手法が「ロジスティック回帰」です。
今回は、ロジスティック回帰の基本概念から実際の活用方法まで、わかりやすく解説していきます。
これらについて、理解が難しい場合は経験豊富な方とマンツーマンで学習していくのもオススメです。
ロジスティック回帰とは
ロジスティック回帰は、結果が2つのカテゴリーに分類される問題(二項分類)を解決するための統計的手法です。
線形回帰との違い
線形回帰は予測値の範囲は特に限りがありませんが、ロジスティック回帰の場合は予測値を確率として出力した上で、2値の値を予測していきます。
| 項目 | 線形回帰 | ロジスティック回帰 |
|---|---|---|
| 目的変数 | 連続値 | 2値(0 or 1) |
| 予測値の範囲 | -∞ ~ +∞ | 0 ~ 1(確率) |
| 関数 | y = ax + b | \( p = \frac{1}{1-e^{-ax+b}} \) |
| 用途例 | 売上予測、気温予測 | 合格判定、病気診断 |
シグモイド関数の役割
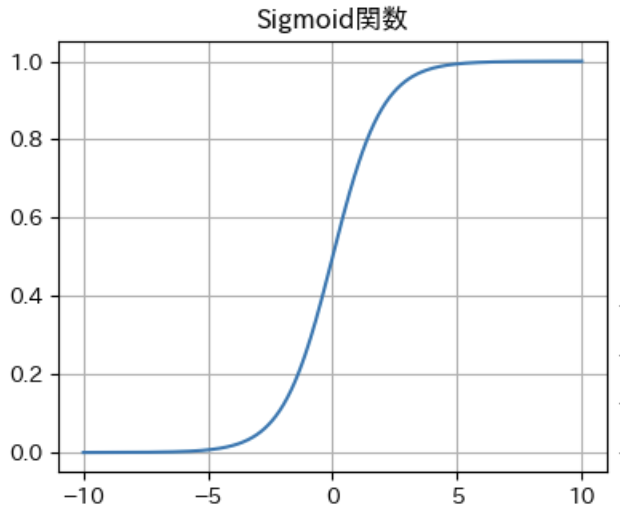
ロジスティック回帰に用いられるのが「シグモイド関数」です。この関数は、任意の実数値を0から1の間の値に変換します。
下記xの部分に重回帰予測のようなy = ax+bなどを入れて、確率を予測していきます。
シグモイド関数:\( f(x) = \frac{1}{1-e^{-x}} \)
予測のプロセス
ロジスティック回帰は下記のプロセスで予測値を算出します。
- 確率計算:シグモイド関数でp(確率)を算出
- 分類決定:閾値(通常0.5)で0/1を判定
- p ≥ 0.5 → 「1」と予測
- p < 0.5 → 「0」と予測
実際の例で理解しよう:学生の合格予測
大学入試の合格予測を例に、ロジスティック回帰の仕組みを見てみましょう。
データ例
| 学生ID | 勉強時間(時間/日) | 模試得点 | 合格(1)/不合格(0) |
|---|---|---|---|
| 1 | 2 | 65 | 0 |
| 2 | 4 | 78 | 1 |
| 3 | 1 | 45 | 0 |
| 4 | 6 | 85 | 1 |
| 5 | 3 | 70 | 0 |
| 6 | 7 | 92 | 1 |
| 7 | 5 | 82 | 1 |
| 8 | 2 | 58 | 0 |
モデルの解釈
勉強時間をx₁、模試得点をx₂とすると、合格確率は以下のように表現できます。
例えば、分析結果として以下の係数が得られたとします。
- β₀ = -47.37(定数項)
- β₁ = 0.08(勉強時間の係数)
- β₂ = 0.64(模試得点の係数)
この場合、勉強時間5時間、模試得点74点の学生の合格確率は
閾値を0.5としている場合は合格と判定します。
実装時の注意点
ロジスティック回帰は回帰係数を出力して予測する手法ですので、多重共線性や外れ値などに影響されていないかしっかりと確認する必要があります。
これらを確認して実装しないと信頼性の低い予測となる可能性があります。
まとめ
ロジスティック回帰は、2値分類問題を解決する強力で解釈しやすい手法です。シグモイド関数により確率を予測し定量化できます。
ぜひロジスティック回帰を理解して、様々な二項分類問題に挑戦してみてください。
線形回帰の知識があれば理解しやすく、多くの実用的な問題に適用できる汎用性の高い手法です。
ロジスティック回帰を学ぶのにオススメの方法
書籍:初心者のためのロジスティック回帰入門
ロジスティック回帰の入門本となります。しっかりと理解したい方にオススメです。
スクール:現役データサイエンティストに教えてもらう
ロジスティック回帰はデータ分析で基礎的かつ重要な部分となります。スクールなどに入り、アドバイスしてもらいながら理解して進めるのも良いでしょう。





コメント