統計学で用いられる「尤度」とは。わかりやすく紹介

はじめに

統計学において「尤度（ゆうど）」は、データが観測された際に、そのデータがある特定のモデルやパラメータによってどれだけ「もっとも(尤も)らしい」かを示す指標です。この概念は、特に統計モデルの評価やパラメータの推定において重要な役割を果たします。

尤度は多くの分析の基礎知識となり非常に重要な知識となります。これらの知識を体系的に学んで実務に活用するためには様々な講師と相談しながら進める等もオススメです。

尤度を理解するために、まずは確率の概念から出発しましょう。例えば、サイコロを1回振ったとき、出る目の確率はどれも1/6です。

ここで、「確率」は「事前に知っている情報」に基づいて、ある結果がどれだけ起こりやすいかを示します。一方、「尤度」は、ある結果がすでに観測された場合に、その結果がどのような仮説やパラメータで説明されるかを評価するものです。

具体例として、コインを10回投げたとします。結果として表が7回、裏が3回出た場合、この結果に対する尤度を考えます。ここでは、コインが公正である（表が出る確率が50%）か、もしくは偏っている（表が出る確率が異なる）かを仮定できます。

まず、公正なコインの仮定では、表が出る確率p=0.5とします。この場合、表が7回、裏が3回出る確率（尤度）は以下のように計算できます。

$$ L(p) = P(\text{表が7回、裏が3回}) = {}_{10}C_7 \times (0.5)^7 \times (0.5)^3 $$

次に、表が出る確率が異なる場合、例えばp=0.7という仮定をすると、同じデータに対する尤度は次のようになります。

$$ L(p) = P(\text{表が7回、裏が3回}) = {}_{10}C_7 \times (0.7)^7 \times (0.3)^3 $$

尤度の考え方を最も効果的に活用する方法の一つが「最尤推定」です。この手法では、観測されたデータに対して尤度が最大となるパラメータを推定します。

表が出る確率をpとします。先ほどのコインの例に戻ると、表が7回、裏が3回出た結果に基づいて、最も尤度が高いpを見つけることができます。以下の式を最大化するpを求めます。

$$ L(p) = {}_{10}C_7 \times p^7 \times (1 – p)^3 $$

実際にこのL(p)について、pを変化させていったとき、L(p)が最大となるところを見てみます。

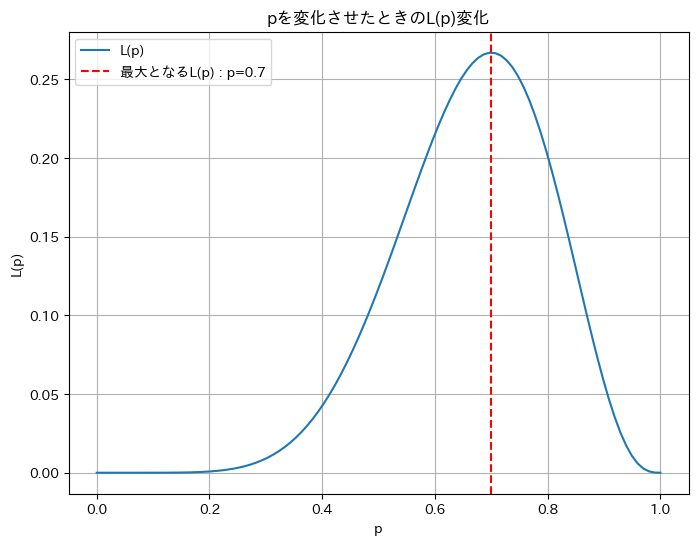
このように10回表が出たとき、表がでる尤もらしいpの値は0.7と算出されます。このように、最尤推定を用いることで、データに最も適したパラメータを推定できます。

尤度は、観測されたデータに基づいて、そのデータを最もよく説明するパラメータを推定するための重要な概念です。最尤推定は、この尤度を最大化するパラメータを見つける手法であり、統計学やさまざまな分野で広く使われています。

尤度は「AICやBIC」、「ベイズ推定」で用いられます。これらは統計モデルの活用において非常に重要な部分となりますので、尤度の概念を理解することで、データ分析やモデルの評価がより深く理解できるようになります。

尤度を体系的に学びたい方には以下の書籍がオススメです。この書籍は尤度の計算方法だけでなくベイズ統計を基礎が分かりやすく記載されているため初級者の方にもオススメです。

created by Rinker

岩波書店

尤度は統計学の中でも非常に重要なパートとなるため、しっかりと学び理解することが重要です。ただ、尤度だけでなく周辺知識を学んでいくことで理解が深まります。下記にオススメの書籍をまとめましたので参考ください。