はじめに
データ分析を始める際、データの基本的な特性を把握することが重要です。記述統計量は要約統計量、基本統計量などとも呼ばれますが、データの分布や傾向、外れ値などを確認できます。
本記事では、記述統計量の基本的な指標やその求め方を初心者にも分かりやすく解説します。
記述統計量とは？
記述統計量とは、データを数値で要約するための指標です。以下のような代表的な指標があります。
- 平均値
- 中央値
- 最頻値
- 分散と標準偏差
これらを用いることで、データの全体像を把握できます。それでは、それぞれの計算方法を具体的に見ていきましょう。
基本的な記述統計量の求め方
代表値
平均値
平均値はデータの中心的な値を示します。
平均値の計算式
平均値の例
データが[10,20,30,40,50]の場合、下記のようになります。
中央値
中央値はデータを昇順に並べた際の中央の値です。データの個数が偶数の場合、中央の2つの値の平均を取ります。
中央値の計算手順
- データを昇順に並べる。
- 個数が奇数なら中央の値を取る。
- 個数が偶数なら中央の2つの値の平均を取る。
中央値の例
データが[10,20,30,40,50]の場合、順番に並んでいる真ん中の値は30になるので、中央値は30。
データが[10,20,30,40]の場合、順番に並んでいる中央の値は20、30になるので、中央値は2つの平均の25。
最頻値
最頻値は、データの中で最も頻繁に現れる値です。
最頻値の例
データが[10,20,20,30,40]の場合、20が最も多く表れているので最頻値は20。
平均、中央値、最頻値の使い分け
- 平均: データ全体の中心傾向を把握したい場合に使用します。ただし、外れ値に影響を受けやすい点に注意が必要です。
- 中央値: 外れ値の影響を避けたい場合や、データが非対称な分布を持つ場合に適しています。
- 最頻値: カテゴリデータや頻繁に出現する値を重視する場合に便利です。
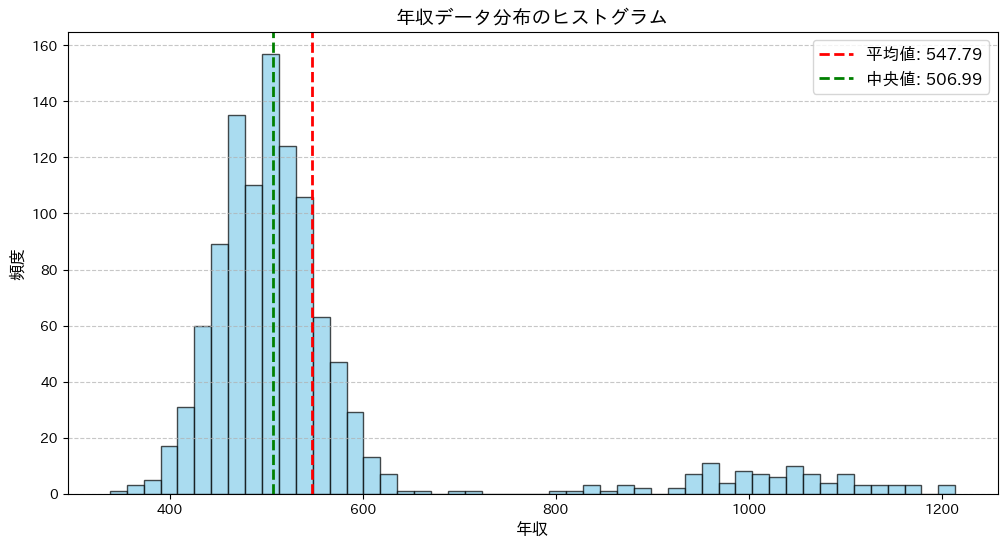
例えば、年収データを見たときに、平均的な年収層(左側)に加えて、年収1000万円以上の層が少数いたとします。
その場合は平均値が高年収層に引っ張られてしまうため、このような場合は平均値ではなく中央値を使う方が代表値としては適切かもしれません。
ばらつきを表す値
分散と標準偏差
分散と標準偏差は、データのばらつきを示すことができます。
分散の計算式
標準偏差の計算式
分散と標準偏差の例
左は分散が低く、右は分散が高いデータとなっています。見て分かる通り、右の方がばらつきが大きいことがヒストグラムから分かります。
まとめ
記述統計量はデータ分析の第一歩として非常に有用です。特に、平均値や中央値、標準偏差といった基本的な指標を理解し、活用することで、データの特徴を簡単に把握できます。データの傾向や外れ値を確認する際には、記述統計量を積極的に活用しましょう。
記述統計量を学ぶのにオススメの方法
書籍：統計学入門
初学者が記述統計量に加えて、統計学を網羅的に学ぶには下記の書籍がオススメです。多くの図が含まれているため、初学者であっても非常に理解しやすいです。
スクール：現役データサイエンティストに教えてもらう
記述統計量はデータ分析で基礎的かつ重要な部分となります。ただ、どのようにやるのが正しいのかを理解しながら進めるには適切なメンターなどがいた方が安心です。スクールなどに入り、アドバイスしてもらいながら進めるのも良いでしょう。
コメント