はじめに
コレスポンデンス分析(Correspondence Analysis, CA)は、2つのカテゴリ変数の関係を、クロス集計表 → 2次元プロットに変換して見える化する手法です。
マーケティング調査では「商品属性 × 年代」「ブランド × イメージ語」などの対応関係を読み解くのに使われます。
コレスポンデンス分析はマーケット調査などを実施する際に非常に有効な手段となります。しかし、もしこれらについて理解が難しい場合は、経験豊富な方とマンツーマンで学習していくのもオススメです。
コレスポンデンス分析とは
コレスポンデンス分析は、2つの変数がどのように関連しているかを可視化するための手法です。
主にマーケットリサーチなどで用いられ、クロス集計表を2次元プロットすることで、カテゴリAとカテゴリBの関係性を把握することができます。
クロス集計のみの場合
一般的なクロス集計表だと下記のように数値だけ並べられるため、どのような傾向があるかすぐに判断できません。
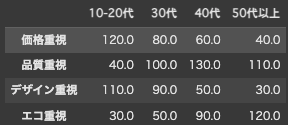
クロス集計をグラフにする:コレスポンデンス分析
ただこのクロス集計表をグラフにしてどのような傾向があるかをに理解するために使われるのがコレスポンデンス分析です。テーブルと比べて、どの年代がどんな傾向があるか、すぐにわかることができます。
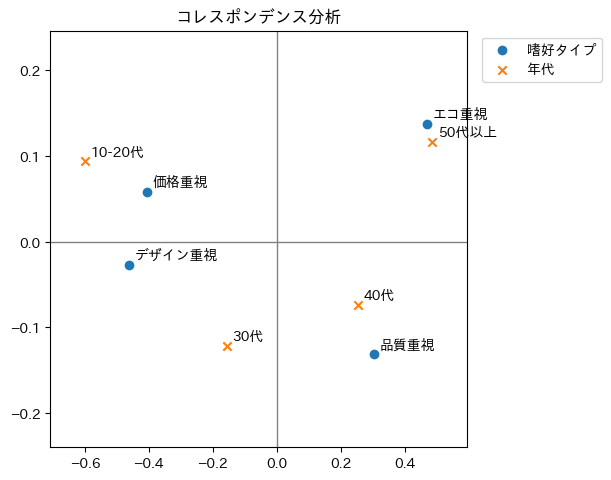
- 50代以上はエコ重視そうだ。。
- 40代は品質重視みたいだ。。
などがこの2次元グラフからグラフィカルに見えれば、分析の幅も広がりそうです。よくマーケットリサーチの分析に用いられます。
コレスポンデンス分析の流れ
流れは大まかに下記になります。クロス集計表さえあればコレスポンデンス分析を実行することができます。
- データから行方向には変数A、列方向には変数Bのカテゴリを配置し、クロス集計表を作成する。
- クロス集計表からコレスポンデンス分析を実行する。さまざまな分析ツールに組み込まれていることも多いのですが、下記の通りでPythonでも実施可能です。
ただ、この理論的な数式は結構細かいのですが、もし数式で理解したい方にはこちらがオススメです。
コレスポンデンスをpythonで実装する
下記がpythonの実装となります。
mcaのpackageを使うことで簡単にコレスポンデンス分析を実装できます。
import mca
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# ===== データ準備:行=嗜好タイプ、列=年代、値=件数(クロス表) =====
row_labels = ["価格重視", "品質重視", "デザイン重視", "エコ重視"]
col_labels = ["10-20代", "30代", "40代", "50代以上"]
table = np.array([
[120, 80, 60, 40], # 若年層に価格重視が多い
[ 40, 100, 130, 110], # 中高年層に品質重視が多い
[110, 90, 50, 30], # 若年〜30代にデザイン重視が多い
[ 30, 50, 90, 120], # 高年層にエコ重視が多い
], dtype=float)
df = pd.DataFrame(table, index=row_labels, columns=col_labels)
# ===== コレスポンデンス分析 =====
ca = mca.MCA(df, benzecri=False)
row_scores = ca.fs_r(N=2)
col_scores = ca.fs_c(N=2)
# === グラフの作成 ===
fig, ax = plt.subplots(figsize=(6, 6), constrained_layout=True)
# 行カテゴリ
ax.scatter(row_scores[:, 0], row_scores[:, 1], marker='o', label='嗜好タイプ')
for label, x, y in zip(df.index, row_scores[:, 0], row_scores[:, 1]):
ax.annotate(label, (x, y), xytext=(4, 4), textcoords='offset points')
# 列カテゴリ
ax.scatter(col_scores[:, 0], col_scores[:, 1], marker='x', label='年代')
for label, x, y in zip(df.columns, col_scores[:, 0], col_scores[:, 1]):
ax.annotate(label, (x, y), xytext=(4, 4), textcoords='offset points')
# 原点線
ax.axhline(0, linewidth=1, color='gray')
ax.axvline(0, linewidth=1, color='gray')
# 調整
xs = np.r_[row_scores[:, 0], col_scores[:, 0]]
ys = np.r_[row_scores[:, 1], col_scores[:, 1]]
pad = 0.1 * max(xs.max() - xs.min(), ys.max() - ys.min())
ax.set_xlim(xs.min() - pad, xs.max() + pad)
ax.set_ylim(ys.min() - pad, ys.max() + pad)
ax.set_box_aspect(1)
ax.legend(loc='upper left', bbox_to_anchor=(1.02, 1))
ax.set_title("コレスポンデンス分析")
plt.show()まとめ
コレスポンデンス分析は、2つの変数がどのように関連しているかを可視化するための手法です。マーケットリサーチなどで用いられ、クロス集計表を2次元プロットすることで、カテゴリAとカテゴリBの関係性を把握することができます。
エクセルを多く使うビジネスマンはピボットテーブルなどを用いて集計表を作ることも多いですが、今回のコレスポンデンス分析をすると一歩上のグラフィカルな分析ができ、新しい施策につながる可能性もあるので、ぜひ活用してみてください。
コレスポンデンス分析にオススメの書籍
例題とExcel演習で学ぶ多変量解析 因子分析・コレスポンデンス分析・クラスター分析
こちらの書籍は実際の実践例などを示しながらコレスポンデンス分析などを学んでいくことができます。
他にもクラスター分析などかなり有用な手法を学ぶことができるためおススメです。




コメント