はじめに
ベイズの定理は、確率論において非常に重要な考え方であり、特に条件付き確率と深い関係があります。この記事では、条件付き確率を通じてベイズの定理の意味をわかりやすく説明し、その例を紹介します。
ベイズの定理は、様々な場面で使われるベイズ推定に必要な知識です。この部分は非常に複雑で難しい部分ですが、これらについて理解が難しい場合は、経験豊富な方とマンツーマンで学習していくのもオススメです。
条件付き確率とは
条件付き確率とは、ベイズの定理を学ぶ前に知っておくべき知識となります。条件付き確率とはある事象が起こるという前提のもとで別の事象が起こる確率を表します。この確率は、「与えられた情報」に基づいて特定の事象の発生確率を計算するものです。
条件付き確率は次のように表されます。
ここで、\( P(A|B) \)は「Bが起きたという前提でAが起きる確率」、\( P(A \cap B) \)は「AとBが同時に起きる確率」、そして\( P(B) \)は「Bが起きる確率」です。
条件付き確率の例
学生が100人いたとして、
- ジュースが好き40人
- お茶が好き30人
- ジュースとお茶どちらも好き:10人という場合を考えます。
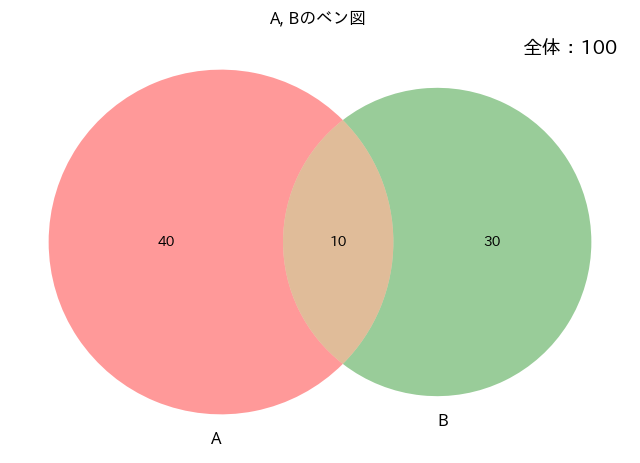
上記の場合は、
- \( P(A) = (40+10) / 100 = 0.5 \)
- \( P(B) = (30+10) / 100= 0.4 \)
- \( P(A \cap B) = 10/100 = 0.1 \)
となりますので、
となります。
ベイズの定理とは
ベイズの定理
ベイズの定理は、次のように表されます。
ベイズの定理の算出
この式は、\( P(A|B) \)と\( P(B|A) \)から共通項の\( P(A \cap B) \)を基に組み合わせればすぐに算出されます。
ここから、ベイズの定理式が算出されます。
まとめ
ベイズの定理は、条件付き確率の基礎から簡単に証明できる重要な法則です。この定理は、新しい情報が与えられたときに確率をどのように更新すべきかを示しており、幅広い分野で応用されています。証明を通じて、その背景にある考え方を理解することで、ベイズの定理がより身近に感じらます。
ベイズの定理を学ぶのにオススメの方法
書籍:市場最強図解 これならわかる!ベイズ統計学
ベイズの定理を体系的に学びたい方には以下の書籍がオススメです。多くの例が書かれており、実際の計算方法と使い方をイメージすることができます。
スクール:現役データサイエンティストに教えてもらう
ベイズの定理はベイズを用いた予測などで理解が必要になります。難しいと感じる場合は、相談しながら進められるスクールもオススメです。





コメント